Standard Deviation in Trading: Calculations, Use Cases, Examples and More – Part I

Whether you’re a seasoned trader or just starting in quantitative finance, grasping the concept of standard deviation is crucial. Standard deviation helps traders with volatility measures in finance. With this helpful tool, traders can make sense of market fluctuations and manage risks effectively.

In this blog, we break down the idea of standard deviation by imparting all the necessary information related to standard deviation in the trading domain. Let’s dive into the exciting journey of understanding standard deviation’s role in trading as we cover:

• What is standard deviation?
• Formula of standard deviation
• How to calculate standard deviation?
• Examples of applications of standard deviation
• Use cases of standard deviation
  • Risk assessment
  • Volatility analysis
  • Portfolio management
• Essential components of standard deviation
  • Unit of standard deviation
  • Standard deviation vs variance
  • Standard deviation for sample data – Bessel’s correction
• Standard deviation in trading as a measure of volatility
• Computing annualized volatility of stocks using Python
  • The z-score
  • Value at Risk
  • Confidence intervals
• Real-world Case Studies of standard deviation
  • Application in Different Markets
  • Impact on Trading Decisions
• Correlation of standard deviation with other indicators
• Limitations of standard deviation in trading
• Common misconceptions about standard deviation in trading
• Risk management tips using standard deviation

What is standard deviation?

Let us see a famous quote defining standard deviation by John Bollinger, a well-known figure in the trading world, primarily recognised for developing the widely-used technical analysis tool known as Bollinger Bands.

“Standard deviation is a key tool for traders to quantify the uncertainty and risk in the market. It allows us to better understand the potential variability of returns and make informed decisions to manage our portfolios effectively.” – John Bollinger

Definition of standard deviation“The standard deviation (σ) is a measure that is used to quantify the amount of variation or dispersion of data from its mean.”

Let’s simplify the concept of deviation from the mean.

In essence, deviation refers to how far a data point is from the average. Imagine we have a set of observations represented by the variable X, consisting of various values: x₁, x₂, …, xn.

Now, let’s consider two of these observations (as shown in the image below), x₁ and x₂, and their deviations from the mean of X.

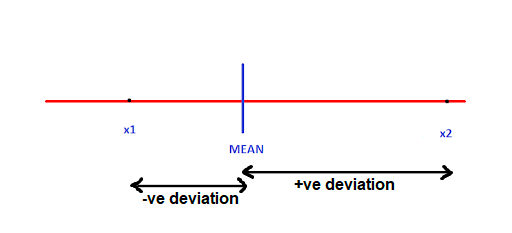
Deviations are straightforward: they tell us if an observation is above or below the mean, shown by positive or negative values respectively.

What if we add up all these deviations?

Interestingly, they would balance out to zero due to the mix of positive and negative values. To overcome this, we square each difference to remove the sign and find their average. This yields the variance, indicating how spread out the data is.

Standard deviation, derived from the variance, provides a standardised measure of dispersion. It involves taking the positive square root of the variance. This process ensures we’re dealing with values in the same units as the original data. In the following section, we’ll delve into the formula for calculating standard deviation.⁽¹⁾

Formula of standard deviation

The formula for calculating the standard deviation (denoted by σ) is as follows:

Going forward, we will discuss the calculation of standard deviation.

How to calculate standard deviation?

To calculate the standard deviation using Python, you can utilise libraries such as pandas and numpy. Here’s a step-by-step guide to calculate the standard deviation using historical price data:

Step 1: Install Required Libraries and import packages

If you haven’t already installed numpy, you can install it using pip:

import numpy as np

Import_libraries.py hosted with ❤ by GitHub

Step 2: Define an example data

Here we have taken an array of numbers to show the calculation.

# Define your data as an array of numbers
data = [10, 15, 20, 25, 30]

Data.py hosted with ❤ by GitHub

Step 3: Compute Standard Deviation

# Compute Standard Deviation
data_std_dev = np.std(data)

print("Standard Deviation of Data:", data_std_dev)

Compute_sd.py hosted with ❤ by GitHub

Output:

Standard Deviation of Data: 7.0710678118654755

We will now discuss some examples of the applications of standard deviation in general as well as in trading.

Examples of applications of standard deviation

Let us check out the general examples of applying standard deviation before heading to the trade oriented example.

General examples

The term standard deviation sounds like something you hear in a statistics class, but don’t dismiss it as an overly technical term just yet. It can be used in different aspects of our lives.

A teacher can use the standard deviation of marks of her students in an exam as a metric to assess the overall level of understanding of the subject. If the mean and standard deviation are both high, it indicates that, on average, students have a good understanding of the subject.

However, there would be many students who have scores that are much above and much below the average scores. In case the mean is high and the standard deviation is low, it indicates that the average scores are similar to the previous case.

The low standard deviation tells her that most students have scores that are close (i.e. slightly above and slightly below) to the mean. In weather forecasting, it can be used to compare the weather patterns in two or more regions.

If we compare the standard deviation of temperatures in Jaisalmer (which has extreme weather) with Mumbai (which has moderate weather), we would find that the former has more variability in temperature around the mean.

Examples of application in trading

Example: Amazon (AMZN) Stock

• Volatility Analysis: Traders analysing Amazon’s stock may calculate the standard deviation of its daily returns over a specific period, such as the past year. A higher standard deviation indicates greater price volatility, implying larger price swings.
  For instance, if Amazon’s stock has a daily standard deviation of 2% over the past year, it suggests that, on average, the daily price movements deviate by 2% from the mean daily return.
• Options Trading: Standard deviation is a crucial factor in options pricing models like the Black-Scholes model. Traders estimating the implied volatility of Amazon’s options contracts may use historical standard deviation as a reference point.
  For instance, if the historical standard deviation of Amazon’s stock is 20% and the implied volatility of its options is significantly higher, it might suggest that options are relatively expensive, potentially presenting trading opportunities.
• Risk Management: Investors holding Amazon’s stock in their portfolio may use standard deviation to assess and manage risk. By calculating the standard deviation of Amazon’s daily returns, investors can estimate the potential range of price movements and set stop-loss orders or position sizes accordingly.
  For instance, if an investor is comfortable with a certain level of risk, they may adjust their position size based on Amazon’s historical standard deviation to align with their risk tolerance.

Use cases of standard deviation

Here are the use cases of standard deviation in risk assessment, volatility analysis, and portfolio management:

Risk Assessment

• Credit Risk Evaluation: In financial institutions, standard deviation is used to assess the variability of returns on loans or investments. A higher standard deviation indicates higher volatility, implying greater risk. Lenders may use standard deviation to evaluate the creditworthiness of borrowers and determine appropriate interest rates.
• Market Risk Management: Standard deviation helps quantify market risk by measuring the variability of asset prices or portfolio returns. Traders and investors use standard deviation to assess the potential downside risk of their investments and implement risk mitigation strategies accordingly.

Volatility Analysis

• Options Pricing: Standard deviation is a key input in options pricing models like the Black-Scholes model. A higher standard deviation implies higher implied volatility, leading to higher option premiums. Traders use standard deviation to estimate the future volatility of underlying assets and determine the fair value of options contracts.
• Technical Analysis: Standard deviation is used to calculate volatility indicators such as Bollinger Bands. These bands consist of a moving average and upper and lower bands representing standard deviations from the mean. Traders use Bollinger Bands to identify potential buy or sell signals based on volatility levels.

Portfolio Management

• Diversification: Standard deviation is used to measure the risk of individual assets and portfolios. By diversifying investments across assets with low or negatively correlated returns, investors can reduce portfolio risk. Standard deviation helps investors assess the effectiveness of diversification strategies and optimise asset allocation to achieve desired risk-return profiles.
• Risk-adjusted Performance: Standard deviation is used to calculate risk-adjusted performance measures such as the Sharpe ratio and the Sortino ratio. These ratios quantify the excess return generated per unit of risk (measured by standard deviation). Portfolio managers use these metrics to evaluate investment strategies and compare the risk-adjusted returns of different portfolios.⁽²⁾

Let us now head to the essential components concerning standard deviation that are used in the calculation part.

Essential components of standard deviation

Let us now see the essential components that are required for calculating standard deviation in the trading domain.

These are:

Unit of standard deviation

The unit of standard deviation would be the same as the unit of our data. This makes it easier to interpret compared to the variance. In the next section, we do a detailed comparison between these two measures of dispersion.

Standard deviation vs Variance

As we can see, by its very construction, the variance is in the square of the original unit. This means that if we are dealing with distances in kilometres, the unit of variance would be in square kilometres.

Now, square kilometres may be easy to visualise as a unit, but what about year2 or IQ2, if we are working with ages or IQs of a group? They are harder to interpret. Hence, it makes sense to use a measure that can be comparable to the data on the same scale/units, like the standard deviation.

Standard deviation is calculated as the square root of variance. It has the same unit as our data and this makes it easy to use and interpret. For example, consider a scenario where we are looking at a dataset of the heights of residents of a neighbourhood. Assume that the heights are normally distributed with a mean of 165 cm and a standard deviation of 5 cm.

We know that for a normal distribution,

• 68% of the data points fall within one standard deviation,
• 95% within two standard deviations, and
• 99.7% fall within three standard deviations from the mean.

Thus, we can conclude that the height of almost 68% of the residents would lie between one standard deviation from the mean, i.e., between 160 cm (mean – sd) and 170 cm (mean + sd).⁽³⁾

Standard deviation for sample data – Bessel’s correction

When calculating the standard deviation of a population, we use the formula discussed above. However, we modify it slightly when dealing with a sample instead.

This is because the sample is much smaller compared to the entire population. To account for differences in a randomly selected sample and the entire population, we ‘unbias’ the calculation by using ‘(n-1)’ instead of ‘n’ in the denominator of equation 1. This is referred to as Bessel’s correction.⁽⁴⁾

Thus, we use the following formula to calculate the sample standard deviation (s).

Stay tuned for the next installment to learn about standard deviation in trading as a measure of volatility.

Author: Chainika Thakar (Originally written by Ashutosh Dave and Udisha Alok)

Originally posted on QuantInsti blog.

Go Source