Expected Shortfall (ES)

The article “Expected Shortfall (ES)” was originally posted on QuantInsti blog.

If you are reading this blog, this means that you are aware of Value at Risk, or simply VaR which is the largest loss that can be incurred by a portfolio with a given confidence level (i.e. a pre-specified probability level).

However, there is a significant drawback which the VaR as a risk measure carries. In particular, it tells us the threshold of potential loss but not how bad the loss can be beyond that threshold.

For example, if a portfolio’s 1-day VaR is $1 million at a 95% confidence level, you don’t know how much the loss could be in the remaining 5% of the cases. In addition, it does not account for “tail risk” or extreme events that may lead to larger losses. This brings us to yet another statistical risk measure called Expected Shortfall (ES), which fixes this problem to some extent.

As seen in the preceding paragraph, to be fully equipped to understand the topic of Expected Shortfall, first one needs to have the knowledge of VaR. What follows is the list of prerequisites needed alongside their descriptions.

Prerequisites

1. The introduction to VaR is explained here. By reading the referred blog, you will learn how to compute and interpret portfolio VaR, its limitations and advantages in simplest and shortest possible way.
2. To get a comprehensive knowledge about VaR and related topics, you can refer to the blog “Value at Risk”. Here you will find a detailed explanation of VaR, its computation in various ways. In addition, this blog provides a coverage of topics like Marginal VaR, Incremental VaR and Component VaR. In short, these VaR tools measure the effects of changing portfolio positions on existing portfolio VaR.

What is Expected Shortfall (ES)

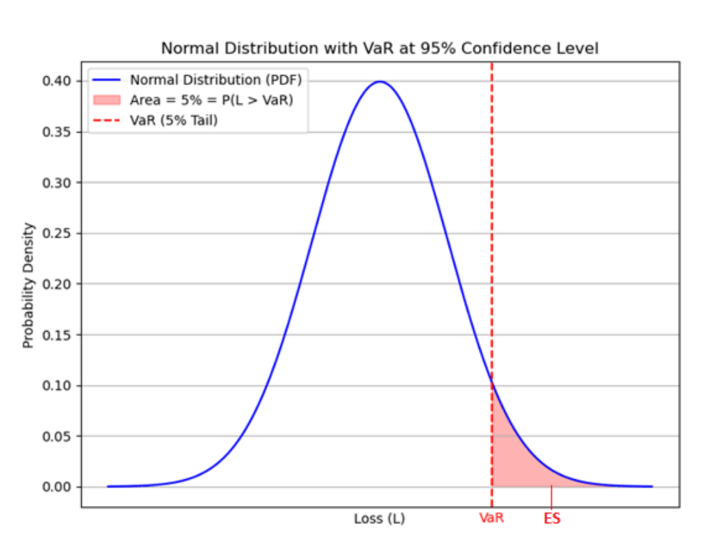
Simply put, Expected Shortfall is the average loss beyond VaR. It measures the expected loss in the tail of a distribution beyond a certain quantile level (e.g., 95%). It provides insight into the potential losses exceeding the Value at Risk (VaR). Obviously, we specify the confidence level by which ES is computed. Below is the geometric illustration of ES alongside with VaR. Here are the steps for the computation of ES:

1. Define Parameters

• Confidence Level (c): Choose the confidence level, typically 95% or 99%.
• Loss Distribution: Have the historical or simulated distribution of portfolio returns or losses.
• Calculate portfolio value at risk (VaRp): This is also computed by the same confidence level.

where z stands for standard normal quantile corresponding to c probability, p is the standard deviation of portfolio returns and W represents the portfolio value in dollars.

2. Calculate Expected Loss Beyond (VaR): This is in effect the Expected Shortfall and is computed by the formula

where LL denotes the loss as a random variable (i.e. the possible value of actual loss). The above formula is read as the expected (average) loss given that this loss is greater than VaRp.

The formula of Expected Shortfall is a theoretical one. We take empirical (historical data based) and analytic approaches to compute this quantity.

Empirical Approach:

The simplest way to compute the ES from historical data is to find VaR using the non-parametric method. As long as VaR is computed, one needs to simply average out all historically observed values beyond this quantity.

Example:

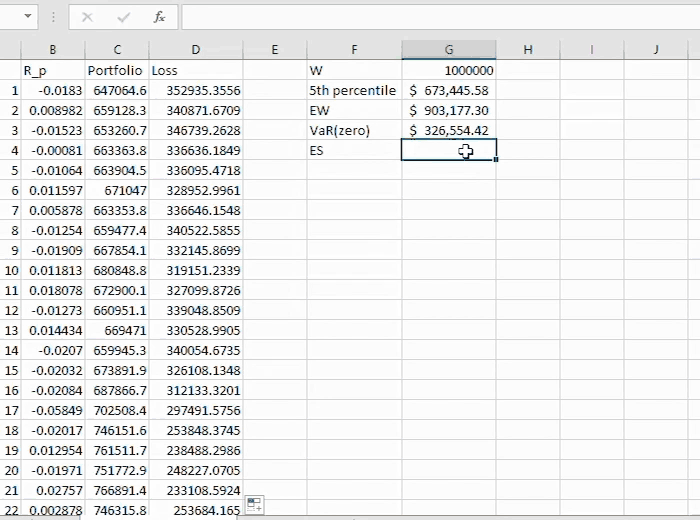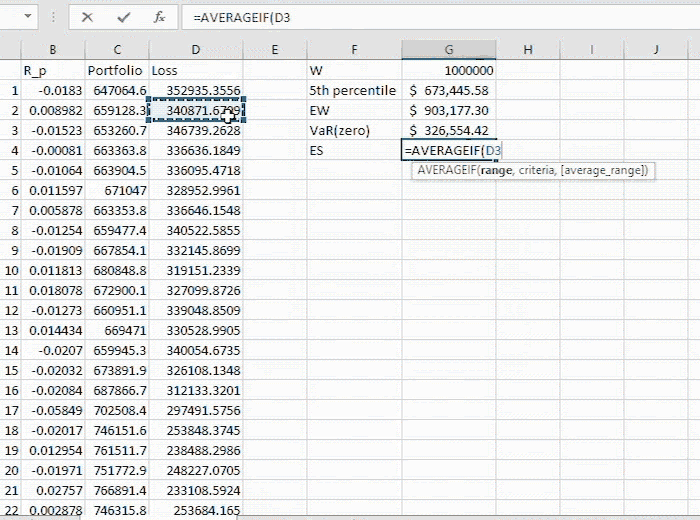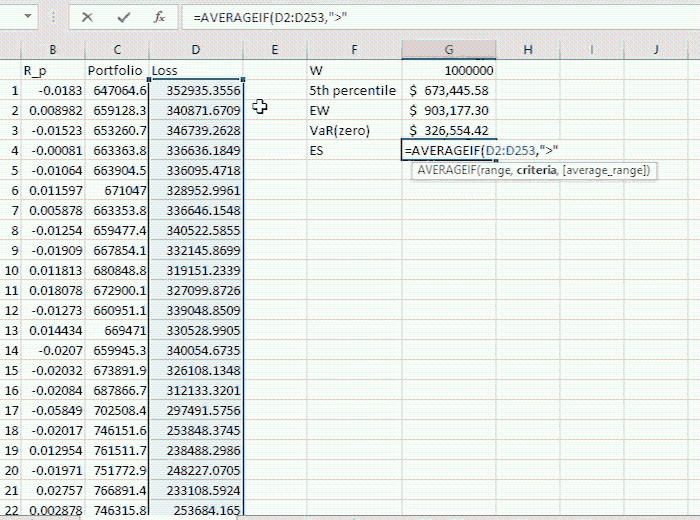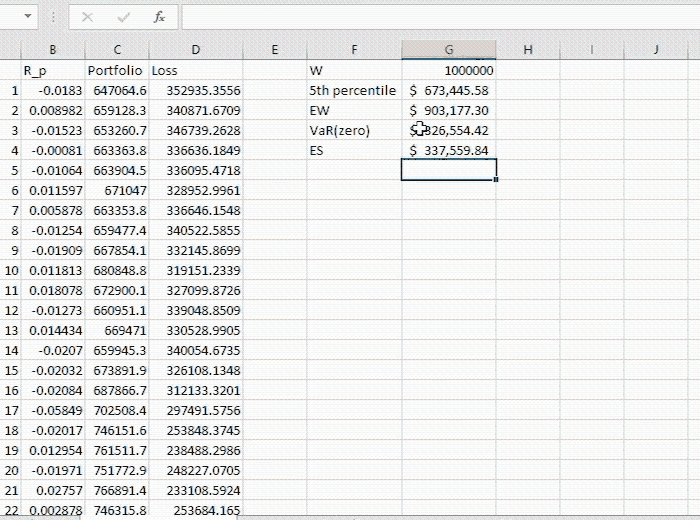
We extend the example given in the section “Non-Parametric VaR” of blog Value at Risk. In particular, as long as the annual VaR (in this case we use VaR (zero), however VaR (mean) would also work) has been computed, we compute the average value of losses beyond this level. Note that these quantities are computed in the blog on the given link above. See the attached Excel file for full computations as well.

The given portfolio in this example is initially worth $1,000,000 and it consists of three assets. First, the portfolio values are computed.

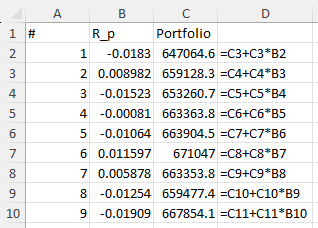
Then we compute the loss incurred compared to the initial value of the portfolio.

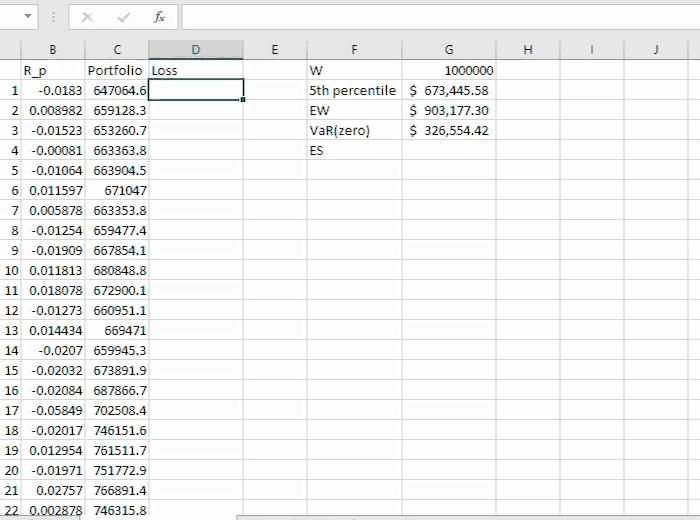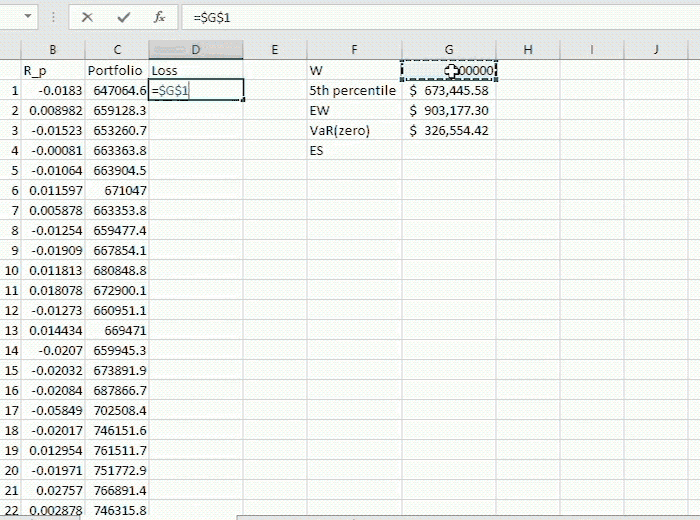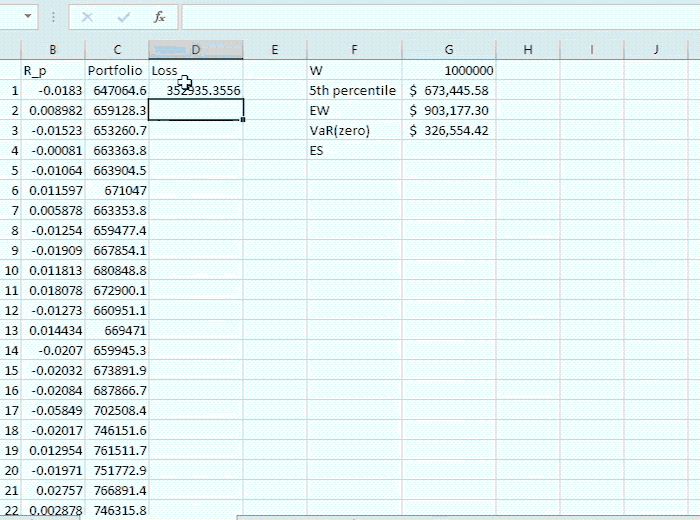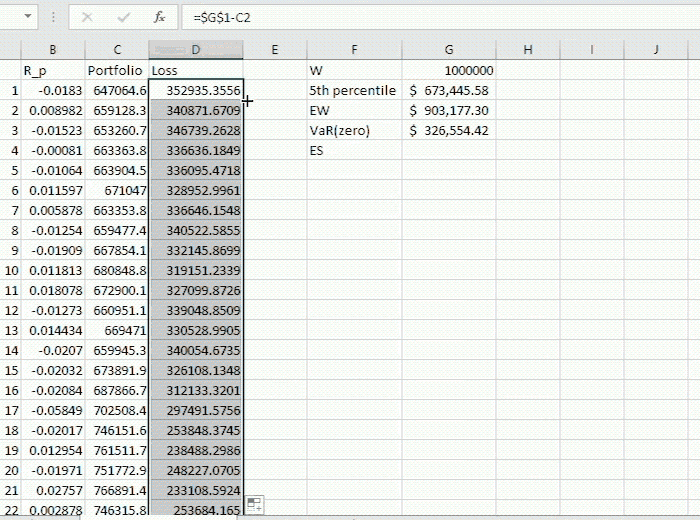
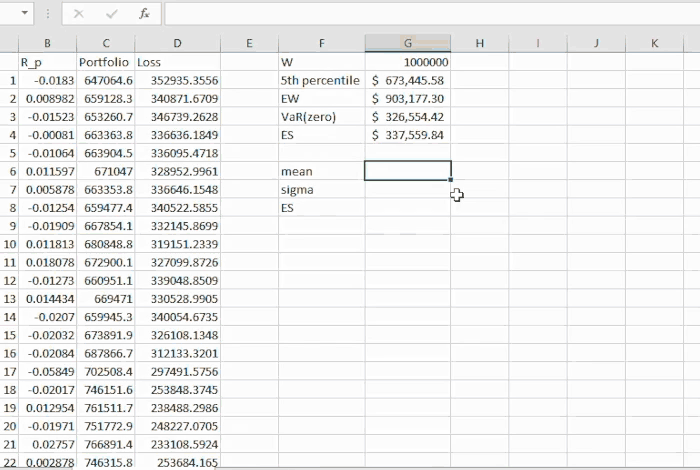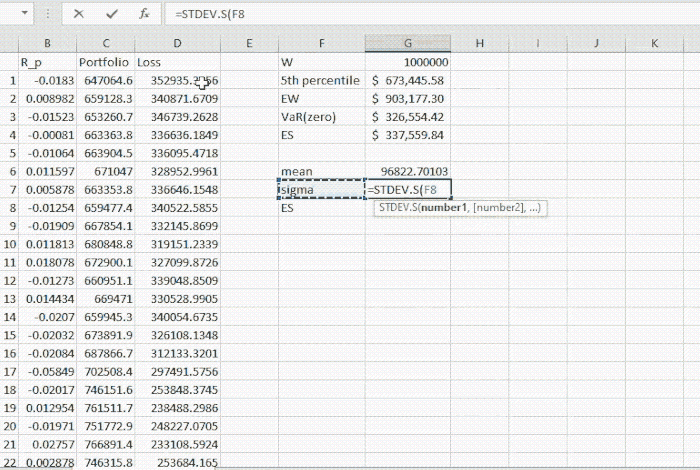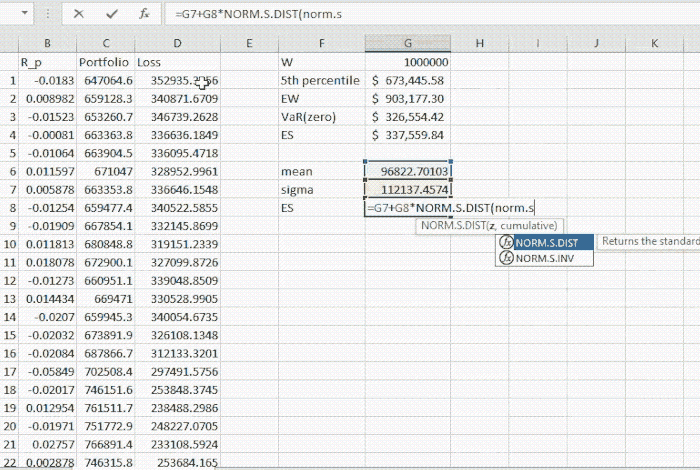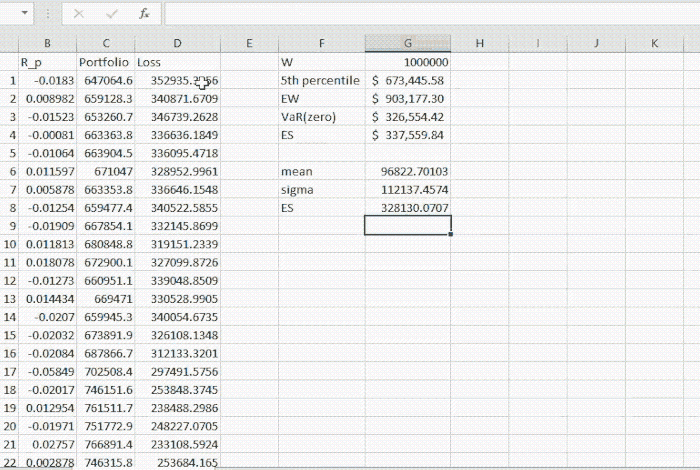
The VaR turns out to be $326,554.42 (computed in the blog above) while the Expected Shortfall is $337,559.84. This quantity is computed by (2) as illustrated below

We interpret this quantity as the expected loss in extreme circumstances. To make it clearer and simpler, $337,559.84 is the expected amount if the actual loss surpasses $326,554.42 (the VaR). This is a self-explanatory number in the sense that it provides an impression about what to expect in extreme cases, i.e. if the 5% probability of loss exceeding VaR is realised.

import numpy as np
import pandas as pd
import yfinance as yf
from scipy.stats import norm

# Download the data
amzn = yf.download('AMZN', '2023-11-30', '2024-11-30')
tsla = yf.download('TSLA', '2023-11-30', '2024-11-30')
aapl = yf.download('AAPL', '2023-11-30', '2024-11-30')

# Extract only closing prices
amzn_close = amzn['Close']
tsla_close = tsla['Close']
aapl_close = aapl['Close']

# Put all three closing prices together
df = pd.concat([amzn_close, tsla_close, aapl_close], axis=1)
df.columns = ['AMZN', 'TSLA', 'AAPL']

# Compute the returns
df['R1'] = -df['AMZN'].pct_change()
df['R2'] = -df['TSLA'].pct_change()
df['R3'] = -df['AAPL'].pct_change()

# Construct the portfolio returns column as a weighted sum of individual asset returns and weights
w = np.array([0.4, 0.3, 0.3])
df['Rp'] = (df[['R1', 'R2', 'R3']] * w).sum(axis=1)
df = df.drop(df.index[0])

# Add the Portfolio column with an initial value of 1,000,000
W = 1000000
df['Portfolio'] = W * (1 + df['Rp']).cumprod()

# Compute losses and add as a column to df
df['L'] = W - df['Portfolio']

# Compute VaR(zero)
VaR_zero = W - df['Portfolio'].quantile(0.05)

# Expected Shortfall
ES = df.loc[df['L'] > VaR_zero, 'L'].mean()

print('Expected Shortfall is: {:.2f}'.format(ES))

Expected_shortfall.py hosted with ❤ by GitHub

Analytic Approach:

Instead of computing ES by non-parametric method, as long as the parameters of loss distribution are estimated, we can compute it via the analytic method. In particular, the ES given by (2) is equivalent to

where l denotes the loss. So this formula just gives the average of the losses beyond VaRp adjusted to the confidence level cc. If the distribution is known, the computation becomes simpler. In the simplest case, assuming the losses are normally distributed (which is quite a basic assumption, not necessarily true though), we compute the ES by the following formula:

where L and L denote the mean and standard deviation of losses respectively. Note that these quantities have the indexes to differentiate them from portfolio return mean and standard deviation. z usually represents the standard normal quantile corresponding to c confidence level and  is the standard normal density function. (Would be great to have a link for probability distributions). The computations are given in the example below

Example cont’d:

Now we compute the ES using the analytic, a.k.a. parametric method. Estimated mean and standard deviations are respectively.

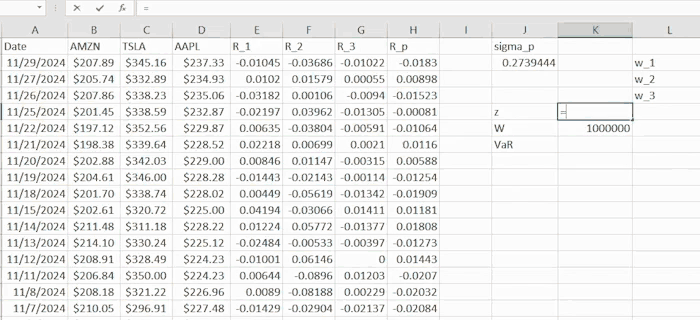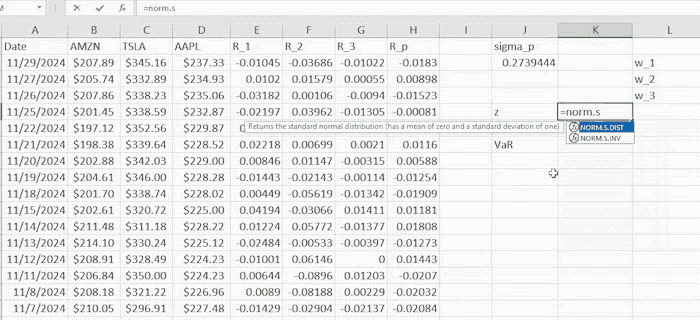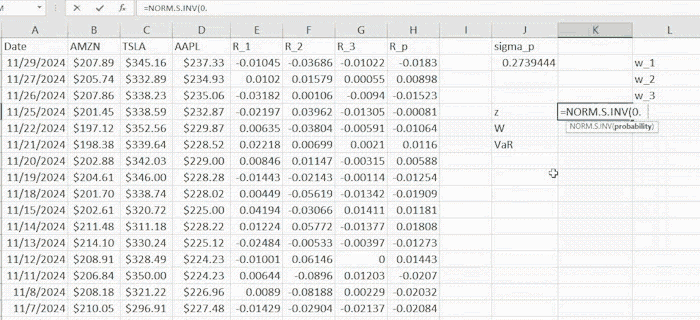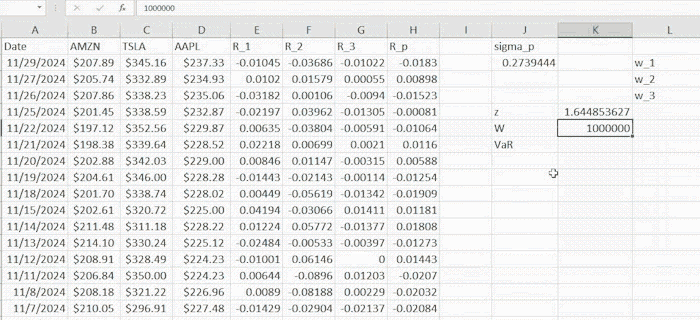
we can compute ES by (4) to be $328,130.07.

Note that this quantity is slightly lower than the ES value computed by non-parametric method, however both certainly are greater than VaR.

import numpy as np
import pandas as pd
import yfinance as yf
from scipy.stats import norm

# Download the data
amzn = yf.download('AMZN', '2023-11-30', '2024-11-30')
tsla = yf.download('TSLA', '2023-11-30', '2024-11-30')
aapl = yf.download('AAPL', '2023-11-30', '2024-11-30')

# Extract only closing prices
amzn_close = amzn['Close']
tsla_close = tsla['Close']
aapl_close = aapl['Close']

# Put all three closing prices together
df = pd.concat([amzn_close, tsla_close, aapl_close], axis=1)
df.columns = ['AMZN', 'TSLA', 'AAPL']

# Compute the returns
df['R1'] = -df['AMZN'].pct_change()
df['R2'] = -df['TSLA'].pct_change()
df['R3'] = -df['AAPL'].pct_change()

# Construct the portfolio returns column as a weighted sum of individual asset returns and weights
w = np.array([0.4, 0.3, 0.3])
df['Rp'] = (df[['R1', 'R2', 'R3']] * w).sum(axis=1)
df = df.drop(df.index[0])

# Add the Portfolio column with an initial value of 1,000,000
W = 1000000
df['Portfolio'] = W * (1 + df['Rp']).cumprod()

# Compute losses and add as a column to df
df['L'] = W - df['Portfolio']

# Compute VaR(zero)
VaR_zero = W - df['Portfolio'].quantile(0.05)

# Expected Shortfall
# ES = df.loc[df['L'] > VaR_zero, 'L'].mean()
# print('Expected Shortfall is: {:.2f}'.format(ES))

ES_analytic = df['L'].mean() + df['L'].std() * norm.pdf(norm.ppf(0.95)) / (1 - 0.95)
print('Expected Shortfall is: {:.2f}'.format(ES_analytic))

Expected_shortfall_ES_analytic.py hosted with ❤ by GitHub

Pros of using Expected Shortfall as a risk measure:

1. Accounts for Tail Risk

• Unlike Value at Risk (VaR), which only considers the threshold loss at a given confidence level, ES averages all losses beyond the VaR, providing a more comprehensive view of tail risk.

 2. Better risk sensitivity

• Unlike Value at Risk (VaR), which only considers the threshold loss at a given confidence level, ES averages all losses beyond the VaR, providing a more comprehensive view of tail risk.

3. Regulatory Acceptance

• ES is increasingly used in financial regulations (e.g., Basel III) because it overcomes some of VaR’s limitations, such as ignoring losses beyond the VaR threshold.

4. Flexibility

• ES can be applied to various distributions and risk scenarios, including heavy-tailed distributions and non-normal data.

Cons and Limitations of using Expected Shortfall as a risk measure:

1. Estimation challenges

• ES requires accurate modeling of the tail of the loss distribution, which is difficult in practice due to the scarcity of extreme loss data.

2. Data and dependence

• Historical and simulation-based methods can produce inaccurate ES estimates if the data does not adequately capture future risk scenarios.

3. Computational intensity

• Calculating ES can be computationally demanding, especially for complex portfolios or when using Monte Carlo simulation.

4. Interpretation complexity

• The choice of the confidence level (c) significantly affects ES, introducing a degree of subjectivity.

5. Sensitivity to model assumptions

• The accuracy of ES depends heavily on the assumed distribution of losses. Mis-specification of the distribution can lead to unreliable estimates.

Conclusion

This blog covered an interesting quantity – Expected Shortfall (ES). ES is the expected loss surpassing the VaR level. It gives a valuable information in the sense that during the realization of extreme losses, one knows what to expect on average. VaR as a risk measure, fails to account for this loss. There are several ways to compute Expected Shortfall. Examples were given illustrating computations of ES by non-parametric method, which gives an estimate using the historical data and an analytic method, which is more robust assuming the distribution of losses is known and the parameters of the distribution (like mean and standard deviation) estimated. Finally, the topic is summarized by providing the list of pros and cons of using ES as a risk measure.

Go Source